
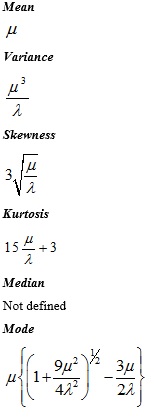
The cell in the 1 st row and the 1 st column of cell range (B3 to B7) is cell B3. This Index function will display the contents of the cell in the 1 st row and the 1 st column of the given range (B3 to B7).

The Index function displays the contents of the cell in the given row (1 st row) and column (1 st column) of the given range. This would have to be the case since only 1 column exists within the given range (B3 to B7).
The column number referenced in this Index function is 1. The row referenced by this Index function is the 1 st row. The row number referenced in this Index function is in cell C10. This is a range of cells that has only 1 column. The Index function has the following syntax:įor the above formula, the range is the cells from B3 to B7. For example, cell D10 contains the Excel formula: The Excel Index function is used in column D to list the city which corresponds to the Distance Chart row number that appears in column C. None of the 5 Decision Variables in this set can be assigned the same number.Ĭolumn D – Listing The Cities Attached To Decision Variables As a result, each 1 of these 5 Decision Variables will be assigned an integer between 1 and 5. This set of 5 Decision Variables are collectively subject to the Alldifferent Constraint. The order of the Decision Variables shown above (1, 2, 3, 4, 5) indicate that the cities will be visited in this order: Boston (row 1 in the Distance Chart) to Chicago (row 2 in the Distance Chart) to Dallas (row 3 in the Distance Chart) to Denver (row 4 in the Distance Chart) to LA (row 5 in the Distance Chart) and back to Boston. These Decision Variables are in cells C10 to C14. In the preceding diagram, the Decision Variables are the row designations of each city. The Decision Variables are the arrangement of the cities to visit. Step 3 – Build the Excel Equations That Combine the Objective With All Decision Variables (Click Image To See an Enlarged Version) In other words, we are minimizing the sum of distances travelled between consecutive cities. We need to determine the order of cities to visit to minimize the total miles travelled. Boston is therefore designated with a “1.” Chicago appears in the 2 nd row in the chart and is therefore assigned a designation of “2.” Dallas appears in the 3 rd row and is designated “3.” Denver appears in the 4 th row and is designated “4.” LA appears in the 5 th row and is designated “5.” The cities are designated in the Excel model not by their names but by the row that they appear in the distance chart just shown.īoston appears in the 1 st row of the distance chart. We are trying to select the order of cities to visit that minimizes the total distance travelled. Step 2 – Determine the Decision Variables The total distance traveled by the salesman is the Objective to be minimized. In this case, the objective is to minimize the total distance traveled when traveling between all 5 cities. He must select the order of customers to visit that will minimize the total length of the trip.īelow is the specific information about the distances between each of the 5 cities:

He must start and finish in his home city of Chicago. The Evolutionary method is used because the mathematical path to the Objective contains the Excel Index lookup function, which is a discontinuous function.Ī travelling salesman living in Chicago must make stops in these 4 other cities: LA, Denver, Boston, and Dallas. The Alldifferent Constraint is used to ensure that the salesman visits each customer only once. A travelling salesman must visit a given number of customers and pick the shortest path that will reach every customer and bring him back to his starting point. This is a classic Solver problem that provides a great opportunity to illustrate the use of the Alldifferent Constraint and the Evolutionary Solver.


 0 kommentar(er)
0 kommentar(er)
